数学の証明が驚くほどできるようになる４つのコツ！

証明問題は避けて通れないが、苦手とする受験生は多い。

普通に方程式を解いたり、積分をしたりといった計算は得意なのに、証明問題になると急に手こずってしまうのだ。

自分で方針を立て、論理をわかりやすく説明する。

そのためには、計算力や思考力以外の力が必要である。

そして、その力は数日で養えるようなものではない。

今回は、証明問題のコツや、それに向けて日頃心がけるべきポイントについて説明する。

今日これを読んだら、早速勉強中に実践してみよう。 日々努力すれば、高得点を取れる証明の書き方がわかってくる。

証明問題を学ぶ意味

まずは、証明問題がどうして必要なのか考えていこう。

勉強する動機があった方が、なによりモチベーションを保ちやすい。

証明問題の勉強はどうして必要で、何の役に立つのだろうか。

差がつく問題

証明問題は、大学のレベルを問わず広く出題されている。

証明とまではいかなくても、大抵の場合途中過程を記すよう要求されるものだ。

証明問題は、計算するだけの問題と異なり面倒だという印象が抱かれがちだ。

それゆえ証明問題というだけで後回しにしてしまう受験生が少なくない。

たとえ証明を書いたとしても、採点官が読んで速やかに理解できる答案でないと、減点されたり、あるいは全く点をもらえなかったりする。

逆に言えば、証明を書く練習を普段から行なっていれば、他の受験生よりも優位に立つことができよう。

したがって、受験数学において証明問題は差がつきやすいのだ。 点数という側面で考えると、証明問題は入試攻略のカギであるといえる。

なぜ証明問題を勉強する必要があるか

後に詳しく述べるが、証明問題は日頃から練習しておかないとなかなか上手なものを書けない。

日頃から雑な答案ばかり書いていると、それが癖になってしまうのだ。

入試で通用する答案を書くためには、やはり普段の勉強が不可欠だ。

センター試験しか受験しないから証明の勉強はいらない、と思う人がいるかもしれないが、それは誤った考えだ。

センター試験でも文章の途中が空欄になっており、そこに数値を入れる必要がある。

どういう意図で計算しているのかを文章から読みとらないと、正しい計算を行えないのだ。

文章を読んで方針を理解するためには、日頃から自分の手で答案を書く練習が不可欠である。

このように、証明の勉強は、証明が入試で登場するか否かに関係なく重要なのである。

数学を受験で使用する以上、避けては通れないものだと認識しておこう。

ここまでのまとめ

ここまでの内容を一旦まとめておこう。 証明問題の勉強は、以下のような理由で大変重要である。

受験生の中には、計算問題ばかりを重視する人がいる。

ベクトル、数列、微分、積分…といった範囲では、確かに計算量が多いので、計算練習は必須だ。

しかし、だからといって証明の勉強を疎かにしてはいけないということを理解してほしい。

「良い証明」って何？

証明問題の重要性を理解したところで、いよいよ本題に入っていこう。

次は、「良い証明」の特徴を探ってみる。

自分の定期試験や模試の答案があったら、それを参照しながら読んでみるとよい。

そうすることで、自分の答案と「良い答案」の違いが見えてくる。

上から読んで理解できる（方針の明快さ）

一つ目の特徴は、「上から順にすんなり読んでいける」ということだ。

証明問題を解く時は、必ずしも「自然な」順に解いていくとは限らない。

たとえば三角形の合同を証明する時に、「何が示せれば合同だと証明できるのか？」という問いを立てて逆算することがよくある。

もちろん、問題を解く際はそれで構わない。

しかし、それを元に答案を書いてしまうのはNGだ。

なぜなら、採点官はあなたの答案を上から順に読むしかないためである。

もちろん、自分自身は証明の概略を理解しているわけだが、採点官はあなたのアイデアを全く知らない状態で答案を読むことになる。

その際、いきなり具体的な計算から入ってしまうと「この計算はどういう意味なんだ？」と思われてしまう。

読者に推測を要求するような答案は試験では絶対NGだ。

逆に言えば、最初に「○○という方針で証明する。」のように方針を明示すれば、これからどのような計算が展開されるのか採点官は理解することができる。

したがって、その後の計算も「なるほどね、ここで余弦定理を使っているわけか…」と思ってもらえる。

方針を明示するだけで、答案の読みやすさは段違いに向上するのだ。

さして大変な作業ではないので、日頃の答案作りの時にどんどん実行してみよう。

計算が冗長でない

後に述べるが、下書きをしないでいきなり答案を書いてしまうとある問題が生じる。

それは、計算の記述が冗長になってしまうことだ。 たとえば、次の答案を見てみよう。

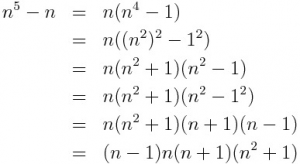＜例題＞ nを自然数とする。このときが30の倍数であることを示せ。 ＜証明＞  と因数分解できる。 以下、nの性質に応じて場合分けしていく。…

上のような答案は、致命的な誤りがあるわけではない。

しかし、ここまで丁寧に式変形をするのは余計である。

これに紙幅を割いてしまっては、30の倍数であることを証明するという最も重要な部分にスペースを割けなくなってしまうためだ。

どういう作業を行ったのか、大まかに分かれば良いので、もうすこし簡潔に記述すべきである。

一つ注意して欲しいのは、上の式変形をいつも省略して良いわけではないということだ。

もし「を因数分解せよ。」という問題だったら、上のような丁寧な記述が要求されるであろう。

大切なのは、今自分が解いているのはどういう問題で、最も注力すべき内容は何なのかを理解することである。

時と場合に応じて、計算は適度に省略するよう心がけよう。

良い答案では冗長な計算過程は排されており、スムーズに読むことができる。

行間が広くない

良い答案として絶対に必要なのが「行間が広くないこと」だ。

ただ、「行間」というのは文字通りの意味ではない。

上で登場した問題の続きを例に考えてみる。

＜上の証明の続き　悪い例＞ さて、は6の倍数なので、あとは5の倍数であることを示せばが30の倍数であることが示せる。…

主張そのものは正しいのだが、問題が一点存在する。

何がまずいのか、採点官になったつもりで一回考えてみてほしい。

読み手の立場で考えるのは、答案作成の際に常に心がけるべきことだ。

問題は、「」が6の倍数になる理由が述べられていないことである。

主張は正しいし、数学的感覚に優れている人であれば直ちに理解できる。

しかし、この事実が成立するのは「自明」とまでは言えず、別途証明を要するのだ。

これが「行間が広い」の意味である。

もっとも、実際は解答欄に制限があるし、最終目標はあくまでが30の倍数であることであるため、次のように軽く理由を述べるだけで良い。

＜上の証明の続き　良い例＞ は、3つの連続した整数である。 したがって2の倍数、3の倍数共に最低1個は含まれており、したがって2×3=6の倍数であるといえる。 が6の倍数なので、あとは5の倍数であることを示せば良い。…

こうすれば、雑な省略は無くなるため、行間が解消されるのだ。 上の悪い例と見比べて、明快さを理解して欲しい。

字が丁寧である

見逃してはならないのが「字の丁寧さ」だ。

読みやすい字であるか否かは、その答案の印象を決定する大切な要素なのである。

「大切なのは見た目でしょ。字の綺麗さはどうでもいいじゃん。」と思うかもしれない。

確かに、核心となるのは答案の内容であり、採点官が評価するのも内容である。

だが、字が汚いと読み手の意欲を削いでしまうのだ。

学校の授業を想像して欲しい。

嫌いな科目の授業を受ける時に、字が綺麗であればある程度頑張る気が起こるだろうが、字が汚いと完全にやる気を失ってしまうのではないだろうか。

判読が難しいと、何となく採点官の気力が失われて、印象が低下してしまう。

部分点を貰えうる答案であっても、判読困難なために点を逃してしまうのだ。

採点官は当然、字の綺麗さで結果が変わらないよう努めているだろうが、こうした事情も考慮すると字を丁寧に書いた方が良いのは明らかだ。

言うまでもなく、芸術的な美しさは要求されていない。

したがって、ずば抜けて綺麗な字を書けなくても落ち込まないで欲しい。

他者に読んでもらうつもりで、自分なりに丁寧に字を書けば良い。

読み手のことを考えた答案作りを目指そう。

「良い証明」の要件まとめ

ここまで、良い答案のエッセンスを紹介してきた。 それをまとめておこう。

これらの点を意識して答案を書くということを肝に命じておこう。

分野に関係なく、証明問題では絶対に必要な条件である。

証明問題の勉強法

どういう証明が良い証明なのか、理解できたにちがいない。

そこで、証明の勉強法について述べていく。

上で学んだことを自分でできるようにするには何をすれば良いのか、明らかにしていこう。

方針を明快にするには

どういう方針で証明するのか。

その方針がわかる答案にすべきである。

数学の参考書が手元にあれば、それを開いて欲しい。

問題の解説の冒頭には、多くの場合「解法のポイント」という形で方針が短くまとめられていることに気づく。

それに相当するものを、自分の答案にも盛り込めば良いのだ。

となると、やることは単純。

証明問題の答案を書く時に、たとえば「部分積分を用いて証明する。」のように一言添えればよいのだ。

いきなり計算から始まるよりも、そういう答案の方が圧倒的に読みやすい。

長い文章で書く必要はない。

最初のうちは、うまく方針を書けない可能性もある。

そういう時は、「余弦定理および正弦定理」のように単語だけ書くようにしよう。

幾度も練習していくうちに、自然な文の書き方が見えてくる。

計算を答案にどう書くか

計算を冗長に書いてはならないと説明した。

それを実践する上で欠かせないのが「下書き」である。

問題が解けた時に、いきなり答案に計算を始めてしまうと、計算過程を全て書き込むことになる。

特に微積分や数列の問題では、計算量が多くなりやすい。

その時に全て答案に書いてしまうと、大幅にスペースが減ってしまうことになる。

その結果、書きたかった文章が書けずに不十分な答案になるのだ。

時間を節約したい気持ちは当然生じるだろうが、そこをぐっと我慢して下書きをする習慣をつけよう。

もちろん、下書きには細かい計算過程を記して構わない。

答案を仕上げる際に、自分で取捨選択すれば良いのだ。

ただし、省略して良い計算と省略すべきでない計算があるので注意しよう。

ただの足し算や引き算などは省略して構わない。

しかし、置換積分のように急に式の形が変わる場合、それを省略してしまうと「この唐突に出てきた新しい文字は何だ？」と思われてしまう。

変化の大きい計算は、省略しないよう注意しよう。

何を省略し、何を残すのか。

その線引きに、初めのうちは苦労することになる。

困った時は、学校の先生にチェックしてもらうと良い。

信頼できる他者によって評価してもらうことで、自分の答案を正しく評価することができるのだ。

行間の広さを解消するには

読み手に推測を要求する、つまり「行間の広い」答案はNG。

それを避けるための特別な方法というものは存在しない。

一つ有力なのは、教科書や参考書の解説を日頃からよく読むことだ。

証明問題でない場合は、答えが合っていれば途中の解説を読まないことが多い。

しかしそれでは、自分の答案が十分詳しいかどうか確かめられない。

教科書や参考書の解説は、そのまま証明として書いても問題ないレベルで詳しいものになっている。

証明問題でなくても、自分のノートとその解説を見比べて、明らかに書いておくべき内容すら省略していたとしたら大いに反省しよう。

答えがあっているか否かは、関係ないとさえ言える。

普段の数学の勉強から、意識的に丁寧に途中過程を書く習慣をつけるのが肝要だ。

そうすることで、証明問題では何を書くべきで何が不要なのか、経験を基に判断できるようになる。

丁寧な字の練習

最後に字の丁寧さだが、これについては平素から努力するほかない。

本番だけ丁寧な字を書こうとしても不可能だ。

やはり、日常のノート作りの段階から、落ち着いて丁寧に字を書くようにしよう。

自分の字は、自分では読めて当然だ。 大切なのは、他者が読めるか否かである。

心配だったら、これもやはり学校の先生に尋ねてみると良い。

あるいは友人のノートや答案を見せて貰おう。

他の人がどういう答案を書いているか実際に見て学べば、目指すべきものが具体的に理解できるにちがいない。

一番大切なのは

証明の書き方にはいくつかポイントがあったが、それを一言でまとめると、やはり 他者が見た時に読みやすい答案を作る ということに尽きる。

相手の気持ちになって考えるという、基本的な考え方に帰着するのだ。

自分でカッとなって作った答案は、自分からしたら努力の結晶かもしれないが、他者が見たらただの汚い答案になっているかもしれない。

客観的な視点で答案を評価できるようになろう。

答案に不安があるときは、先生や友人に答案を見てもらうのが最善の解決策だ。

他者の視点で答案を見てもらうのは、なにも数学に限らず大切なので、忘れないようにしよう。

まとめ

数学の証明問題のコツについて詳しく説明した。

言葉で述べるだけなら簡単だが、いざ自分で証明を書くとなると簡単な話ではない。

とにかく、たくさんの解説を読み、そして自分の手で証明を書いてみよう。

経験値に応じて次第に書けるようになるものだ。

読み手の立場に立って、自分の答案をチェックする。

四つのコツを意識して、満点を取れる答案を目指そう。