数学弱者必見！大学受験数学の４タイプの問題と４段階勉強法

大学受験の数学の成績は、どこで差がつくのだろうか。

同じ教科書や問題集を使って勉強しているのに、定着度・理解度は人によって大きく異なる。

数学の成績がいい人の勉強法を見ても、特別なことをやっているわけではない。

すると、数学で差がつくのは「どういう教材を用いるか」ではなく「どう勉強するか」であることが分かる。

日頃の学習、試験対策、ひいては入試対策につながるような勉強法とはなんなのか。

今回は、理系・文系問わず重要になってくる数学の勉強法について説明していく。 これを読んだら、すぐに実行に移してみよう。

数学はどういう科目か

まずは、数学がどのような科目なのか分析しておこう。 他の科目と何が異なるのか、そして何が要求されているのか。

それを知ることが、適切な勉強法を発見する第一歩だ。

積み上げていく勉強

数学の最大の特徴は、「積み上げ式」の科目である点である。 比較対象として日本史を挙げてみよう。

日本史では様々な歴史上の出来事や人物等を覚えなければならない。

だが、平安時代の歴史がうろ覚えであったとしても、明治時代の勉強をすることは可能だ。

あるいは文化史が苦手であっても政治史が得意、といった受験生は存在する。

もちろん、日本史の知識の全てが独立しているわけではなく、ある程度は関係している。

しかし、分野ごとに別々に勉強していけるのは確かだ。 一方、数学は事情が異なる。

たとえば中学の数学で「二次方程式の解の公式」を我々は学ぶ。 これを理解しないまま先へ進んでしまうと、非常に困ったことになる。 三次関数を微分して極値を求める問題など、二次方程式はあまりに多くの分野で顔を出すのだ。

したがって、二次方程式の解の公式を理解しておかないと、先の内容を学習できなくなってしまうのだ。

こういう意味で、数学は積み上げ式の科目なのである。 理解しきれていないポイントを放置すると、後々必ず痛い目を見る。

「覚えて終わり」ではない

再び日本史と比較してみよう。 たとえば日本史で「文禄の役」について覚えたら、それだけでもある程度の価値がある。

テストでその出来事を問われたら、解答欄に「文禄の役」と記せば点は貰えるからだ。 しかし数学ではそうはいかない。

たとえば余弦定理の式を覚えたとしても、それだけでは点に結びつかない。 実際に問題でその公式を使用できなければ意味がない。

数学では、公式を覚えることではなく、その公式を問題に適用して答えを導く能力が問われているのだ。

言うまでもなく、その運用能力は公式を暗記するだけでは身につかない。 ただ教科書の内容を覚えてはいオシマイ、ではないので要注意だ。

計算も正確性が要求される

数学のもうひとつの特徴は、正確な計算力が要求されているということだ。

当然だと思うかもしれないが、これをおろそかにしていると痛い目に遭う。

数学的な思考力・論証力を有していたとしても、最後の最後で計算ミスをしてしまうと減点対象になってしまう。

問題演習をする際に、計算ミスをあまり気にしない受験生がいるが、これは良からぬ傾向だ。 計算をすることだけが受験数学ではない。

しかし、かといってどうでもよい要素でもないのだ。 計算力は、言ってみれば「前提」である。

大学受験に臨むにあたって、当然のように要求されていることだ。

よって、日頃の学習では思考力だけではなく計算力も養わなければならない。

数学とはどんな科目か

ここまでの内容を一旦まとめておくと、数学という科目には次のような特徴がある。

上のポイントは、理系・文系や受験する大学に関係なく、すべての受験生について言えることだ。 以降これらを肝に命じた上で、数学の勉強法を説明していく。

数学の問題の「タイプ」

数学という科目の性質を理解したところで、次は問題に着目してみよう。

実は、数学の問題にはいくつかの「タイプ」があるのだ。 もし近くに数学の問題集があれば、それを開きながら以下を読んでほしい。

単純1段階タイプ

まずは「単純1段階タイプ」を紹介する。 抽象的な説明を与える前に、問題の具体例を示そう。

＜例題1＞
△ABCにおいて、AB=5、AC=3、∠A=120°であるとき、BCの長さを求めよ。

多くの受験生にとってこれは簡単な問題であり、ものの1,2分で答えを出せるに違いない。

なぜなら、余弦定理をそのまま適用すればすぐに解けるからである。 余弦定理を使う前に、何か準備が必要な訳でもない。

教科書に載っている公式を一回用いればすぐに答えを出すことができるし、与えられている値が限られているので、どの部分で余弦定理を使うのかも一目瞭然だ。

そういう意味で、この問題は「単純1段階的」と言える。 数学の問題演習をするにあたり、まず最初に着手するのはこういう問題であるべきだ。

単純多段階タイプ

単純1段階タイプのような問題は本当に初歩の初歩であり、それだけでは勉強は不十分だ。

次のステップとして「単純多段階タイプ」がある。 次のような問題が良い例だ。

＜例題2＞
二次関数の最小値を求めよ。

これも、高校数学では定番の問題だ。 どの問題集にも必ずこういう問題は載っているので、すでに数学Iを勉強済みであれば楽勝だ。

もちろんaの値によって場合分けをしなければならないため、公式を一回使って終わり、とはいかない。

しかし、場合分けさえしてしまえばあとは単純な最小値問題だ。 一発で終わり、ではないもののやることは明快。

したがって、こうした問題は「単純多段階タイプ」と形容できる。

複雑一段階タイプ

今までに扱ってきた問題は、どれも解法がすぐに定まり、方針を立てるのが容易であった。

複数回の計算が要求されることもあるが、難易度は低い方であった。

次に扱うのは、どういう解法をとれば良いのかすぐにはわからないタイプの問題。

たとえば次のようなものだ。

＜例題3＞
不定積分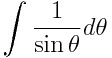を計算せよ。

とにかく上の積分をすれば良いため、目的が非常にはっきりしている。

多くの段階を踏まずに答えにたどり着けるという点は、「単純一段階タイプ」と同じだ。

ところが、多くの受験生にとって上の計算は難しい。 それは、どういう解法で解けばよいのか分からないためである。

この問題のように、段階の数は少ないが解法が直ちに思いつかないものを「複雑一段階タイプ」と呼ぶことにする。

解法が見えにくい分、難しい問題であることは確かだ。 このあたりから、大学入試に登場してもおかしくないレベルになってくる。

複雑多段階タイプ

今までの内容から予測できるだろうが、一番難しいのは、たくさんの手順を踏まなければならない上に解法がわかりにくい問題だ。

これも例を挙げておこう。 実際の大学入試問題から引用することにする。

＜例題4＞ を求めよ。東京工業大学　数学過去問（1988）より

問題文を読むなり、受験生は困ることになる。

なぜなら、2種類の難しさがこの問題には潜んでいるからだ。

一つは「多段階性」、つまりいくつかのステップを経て求めなければならない点だ。

もう一つは「複雑性」、つまり解法を思いつきにくい点である。

具体的な解説は省くが、まず対数をとって、区分求積法を用いて、…というふうに色々手間をかけて計算する必要がある。

こうした問題を「複雑多段階タイプ」と呼ぶことにする。

このタイプが最も難しいというのは想像に難くないであろう。

難関大学であればあるほど、複雑多段階タイプの問題が増えてくるのだ。

まとめ〜問題の分類〜

ここまでの内容をまとめておこう。

数学の問題は、以下の4つに大別できる。

順に難しくなっていく、という理解で構わない。 以下、どういう場合にどのタイプの問題を扱えば良いのかを見ていく。

正しい手順での勉強法

数学の問題は、大きく4つに大別できることがわかった。

解法がすぐに思いつくか否か、そして1ステップで解けるか否か。

それが、問題のレベルを判定する単純明快な方法だ。

数学の勉強をする際には、その分類に注意して、自分に合った問題をチョイスする必要がある。

初学者はどうすべきか

まずは学校の授業前に予習をしている場合や、該当分野の授業が始まったばかりの場合について考えよう。

いってみれば初学者。

何も分からない状態から勉強するのだから、正しい手順を踏まないと挫折することになる。

ゼロから始める場合、4タイプのうちどれから解くべきか。

答えは、言を俟たずして「単純一段階タイプ」である。

なぜなら、そういった問題は教科書に書いてある公式などを使えばほぼ1発で解けるからだ。

そんな簡単なの、やる必要あるの？と思ったとしたらそれは危険な考え方だ。

簡単な問題を解くことで、その定理・公式が何のために存在しているのか、そしてどういう条件のときに用いることができるのかが理解できるのである。

たとえば、余弦定理の公式は少々複雑な形をしており、一見しただけでは意味を理解しにくい。

しかし上の＜例題1＞のような簡単な問題を解くことで、何となく意味が掴めてくるのである。

また、繰り返し演習することで、公式そのものも自然と頭に入るので得ばかりだ。

馬鹿馬鹿しいようでも、初学者はかならず単純一段階タイプの問題に着手しよう。

平易な問題を解くのは、計算練習にも最適だ。

計算力の重要性は前述の通りである。

教科書の例題や練習問題、あるいは教科書の傍用問題集（サクシード、4STEPなど）にこのタイプの問題は多数収録されている。

難しい問題を解きたい気持ちもあるだろうが、そこは一旦冷静になって平易な問題からやってみよう。

公式が馴染んで来たら

ある程度演習を重ねると、単純一段階タイプの問題は一目ですぐに解けるようになる。

それは公式の意味や形が頭に入ってきた証拠だ。

これ以上簡単な問題ばかり解いていても、単純作業の繰り返しになってしまい実りがない。

したがって、次のステップ「単純多段階タイプ」に進んでみよう。

教科書の章末問題や傍用問題集の難しめの問題がこれに相当する。

解法を思いつくのにはさほど苦労しないが、何段階か踏まなければならない問題を解くことで、解法を組み立てていく練習をするのだ。

そうすれば、長い問題にも次第に対応できるようになってくる。

その分野の内容が定着したら

たくさん基礎的な問題演習をすることで、公式の意味や頻出の解法は大抵定着する。

傍用問題集の発展レベルが解けるようになったら、その分野の基礎は完璧になったといって良い。

それだけで、学校の定期試験は楽々突破できるはずだ。

だが、大学入試で要求されているのはさらに上の力だ。

入試では問題の分野が限定されない。

定期試験であれば「微積分」や「ベクトル」など試験範囲が明示されるものだが、入試では全てが試験範囲である。

故に問題の解法も簡単には思いつかない。

複合的（分野横断的）な問題に取り組むことで、様々な問題に柔軟に対応できる力を養う必要が生じてくる。

そういう時に解くべきなのが、先ほど登場した「複雑一段階タイプ」の問題だ。

複雑一段階タイプの問題は、パッと見では解法が分からない。

今までの経験や感覚から判断して、いろいろな手段を試さなければならないのだ。

そういう訓練をすることで、粘り強く解法を探す根気が身につく。

コツとしては、少し考えて分からなくてもすぐには解説を読まないことだ。

実際の入試では、分からないからといって答えを見ることはできない。

独力で解法を探り当てる必要があるのだ。

その練習として、日頃からじっくり考える癖をつけておこう。

このレベルの問題に慣れてくれば、全国模試程度の問題に太刀打ちできるようになる。

そうすれば、いよいよ大学入試の攻略が近づいてくるのだ。

大学入試を突破する力を養う

複雑一段階タイプの問題が解けるようになってきたら、いよいよ最後のステップ「複雑多段階タイプ」だ。

手間もかかるし、解法も難しい。

大学入試で実際に出題されうるレベルの演習をすることになる。

今までとは異なり、一問一問にかかる時間が必然的に長くなる。

大学入試では、大問1つあたり20~30分くらいかかることが多い。

それくらいの時間は継続して考えられる体力を日頃から養っておこう。

先ほど同様、すぐに解説を読まずにひたすら考えることが重要だ。

もちろん入試には時間制限があるので、最終的には素早さも要求されるわけだが、それは本番が近づいてから気にすれば良い。

時間に余裕がある時期は、とにかく自分で色々な解法を試し、独力で答案を作成する経験を積んでおくことがカギである。

その経験値が入試本番で大いに活きることとなる。

題材としては、市販の高難度の問題集でも構わないし、志望大学の過去問でも良い。

自分がギリギリ解けるか解けないかくらいの問題にたくさん取り組むことで、今まで以上の思考力・解答力を鍛えることが可能だ。

まとめ

数学の性質、問題の分類と具体的な勉強方法について説明してきた。

自分がどういう段階にあるにせよ、自分に合ったタイプの問題を演習することが肝要だ。

実力不足なのに難しい問題を解こうとしても実りがない。

焦らずに、1歩1歩着実に前進していこう。

問題のタイプを見極め、適切なものを選んで演習する。

これにより、大学受験の数学の勉強を効率的で着実なものにし、大きな成果をあげてほしい。