本質的な理解へ！物理で微積分を使うメリット・デメリット

高校物理の教科書には微積分が登場しない。

微積分に近い考え方は登場するのだが、多少ごまかして記述されている場合がほとんどだ。

一方、大学以降の物理では微積分が欠かせない。 また、微積分を駆使した方が物理が見えやすくなる部分がある。

そのため、高校物理も微積分を用いて理解しようという考え方をもつ指導者・参考書も存在する。

結局、高校物理では微積分を使った方が良いのかどうか。

理系受験生にとっては気になるポイントであるはずだ。

今回は、高校物理に微積分を持ち込む意義と、どういう人に微積分がオススメかを説明する。

これを読んで、自分にとって最適な物理の勉強法を見つけよう。

そもそもなぜ微積分が登場するのか

受験生の多くは、そもそも物理でどうして微積分が登場するのかピンとこない人が多いに違いない。

そのため、まずは物理においてどうして微積分が登場するのかを見てみよう。

位置と速度、加速度：直線運動を例に

具体的な例で考えてみよう。

質量mの球が、x軸上を直線運動しているとする。

時刻tにおける物体の位置xを、tの関数だと思ってx(t)と表そう。

するとxとtの関係をグラフで表すことができる。

運動が上のように表せるとして、ある時刻t1における物体の速さを求めるにはどうすればよいだろうか。

そのためにはまず「平均変化率」という概念を持ち込んでみる。

時刻の間に物体がどれほど進んだかをグラフで示すと次のようになる。

xの増加量（図の矢印部分）をΔxとすると、これは次の式で表せる。

時間Δtの間にこれだけ進んだわけだから、Δtの間の平均の速さというものを次式で定義できることがわかる。

これは数学IIで登場した「平均変化率」と同じである。 進んだ距離を、かかった時間で割るという明快な考え方だ。

だが、この結果はやや曖昧である。

というのも、この平均の速さは「○時間で○km進んだ」という結果のみから算出された値であり、その場その場での「瞬間の速さ」を示してはいないからだ。

瞬間の速さというのが想像できない人は、車のスピードメータを想像するとわかりやすい。

たとえば2時間で100 km進んだとしたらその車の平均の速さは時速50 kmだが、その途中では時速40 kmのときや時速60 kmのときがあってもおかしくない。

車のスピードメータに速さが表示されるのと同じように、物体の運動にもその瞬間の速さというものがあって当然だ。

上の平均の速さという概念をうまく活用して瞬間の速さを求めることはできないだろうか。

一見難しそうさが、方法が1つある。 それは、Δtを限りなく0に近づけることだ。

勘の良い読者であれば気づいているだろうが、これは「微分」という作業と全く同じである。

時間幅Δtで求めた平均の速さを、Δt→0という極限を取れば、それは時間幅0の平均の速さ、つまり瞬間の速さになる、というのが微分の考え方だ。

つまり、時刻t1での瞬間の速さは

と計算できる。

ここまでの議論は何も時刻t1に限った話ではないので、上の議論から瞬間の速さは

と計算できる。

つまり、物体の速度は、物体の位置を時間tで微分すれば良いのだ！ いままでと同様の議論で、加速度aと速さvの関係も求められる。

すなわち、速さvを時間tで微分してやれば加速度が出てくる。

以上より、位置と速度、加速度に関する重要な関係が明らかになった。

位置を時間微分すれば速度に、速度を時間微分すれば加速度になるのである。

逆に、加速度を時間で積分すれば速度に、速度を時間積分すれば位置になるのである！

この関係は、なにも一次元的な運動に限らず成立するものである。

物体の直線運動と時間の関係を考えることで、位置と速度、加速度の関係がわかった。

力と位置エネルギー：バネを例に

次に、力と位置エネルギーの関係を見てみよう。 高校物理ではおなじみの「バネ」を例に考える。

バネ定数をkとして、自然長からの変位をxとする。

このバネの位置エネルギー（弾性エネルギー）は、物理の教科書では

という公式で紹介されているものの、その理由について詳しく説明してくれることはない。

理由づけをしている教科書もあるが、微積分を使ってはいけないという暗黙のルールのために、いい加減でごまかした説明に止まっている。

しかし、私たちはそれを気にする必要はない。

遠慮なく微積分で解明してみようではないか。

そのためにはまず、位置エネルギーとはなんだったかを思い出す必要がある。

位置エネルギーとは、基準の位置から物体をそこまで持っていくのに必要なエネルギーのことであった。

たとえば地表面を基準として高さhのところに質量mの物体があったとしたら、地表面から重力mgに逆らって高さh持ち上げればよいのだから、位置エネルギーは

と計算できる。

今回考えているのは重力ではなくバネの弾性力なので、それに逆らってどれほどの仕事をしなければならないか計算しよう。

位置エネルギーの基準は自然長、つまりx=0にとる。

ここから位置xまで、弾性力に逆らって物体を手で引っ張ることを考える。

重力の場合と異なり難しいのは、位置によって弾性力が変化することだ。

フックの法則によると、x伸びているバネにかかる弾性力は

なのであった（伸びの方向と逆向きであるという意味を込めてマイナスをつけている）。

したがって、バネが伸びるにしたがって力も増大し、上のように簡単には計算できないことがわかる。

この問題を解決するのがまたしても微積分だ。

ある位置xからx+Δxまで少しだけ物体を動かすことを考えよう。

この間の弾性力は、ほとんどで一定とみて良い。

その弾性力に逆らって距離Δx動かすのだから、外力（手で引っ張る力）がなす仕事は

で与えられることがわかる。

少しずつバネを伸ばしていき、そのたびにuを計算して足し合わせていけば位置エネルギーが求まりそうだ。

ただし、Δxという有限の幅で区切って考えている以上、最終的にはΔxを0に近づける必要がある。

という式を見ればセンスのある読者はわかるだろうが、ここで積分が登場する。

uという量は、に幅Δxをかけたものである。

それを全て足し合わせて幅Δxを0に近づけるのだから、これは積分計算そのものだ。

具体的には次のような積分になる。

この程度の計算は、数学IIを履修済みであれば簡単に実行でき、

となる。

以上より、バネの弾性エネルギーの公式を計算できた。

この問題からわかるように、力を位置で積分すると位置エネルギーになるし、逆に位置エネルギーを位置で微分すると力になる。

ただし、位置エネルギーは力に「逆らって」する仕事なので、式にマイナスがつくことに注意しよう。

実際、上で求められたUを位置で微分してマイナスをつけると

となり、フックの法則と同じ形（弾性力）が現れるのである。

物理と微積分

代表的な例を2つ挙げたが、これ以外にも物理の至るところに微積分は登場する。

いま挙げたのは

だが、他にも

など、枚挙にいとまがない。

高校物理の教科書では微積分が登場しないが、大学以降の物理の本には必ず微積分が登場する。

物理という学問自体、微積分という数学的地盤が欠かせないのだ。

お茶の水女子大学理学部物理学科の柴田文明は、物理における微積分について次のように説明する。

高校と大学との間にあるギャップは相当なもので、高校時代の物理は微分積分法を使わない。

大学が入試問題を作成する際に、かなり気を遣う部分である。

他方、微積分が中途半端なまま大学に入ってきた学生は、古典力学の最初からつまずくことになり、 “補習” が必要となる。

線形代数、微積分は物理を学ぶ上で必須であるからだ。

「数理科学」の柴田文明による特集より

このように、物理において微積分は欠かせないスキルとなっている。

だが、高校物理では教育課程の都合上微積分を用いてはいけないという歪んだ制約が生じているのだ。

一方、上の例で説明したように微積分を使った方が物理の本質的理解が進むのも事実である。

教育課程に素直に従うか、本質的理解を求めて微積分を使うか。

迷っている受験生のために、次は両者のメリット・デメリットを述べよう。

高校物理で微積分を使うメリット

微積分は物理を記述するのに欠かせないものである。

だが一方で、高校範囲であれば別に微積分を用いずとも問題を解くことが可能だ。

では、教科書の範囲を超えて物理で微積分を用いることの利点・欠点は何だろうか。

それを説明していく。

統一的な観点を養う

上で挙げたように、たとえば位置と速度・加速度は時間微分・時間積分という深い関係にある。

これを理解しておくだけで、様々な現象を統一的な観点で記述できるようになるのだ。

たとえば物体の投射を考えよう。

時刻0で原点z=0から鉛直上向きに初速度v0で物体を投射したとき、時刻tでの物体の位置はどうなるだろうか。

これも、微積分を使うことで簡単に解決する。

物体にかかっているのは重力だけなので、時刻tでの速度は

となる。

位置を求めるにはこれを積分すればよく、

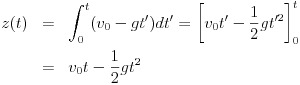
のように求められる。

実行した積分はいたって簡単なもので、理系の受験生ならばまず苦労しない。

この問題に限らず、どんな場合でも位置を時間微分すれば速度を求められるし、速度を微分すれば加速度を求められる。

それを理解した上でもう一度物理の教科書を読み直してみると、実は根底にある原理が本当に少数であることがわかる。

それに気づけたら、高校物理は一気に視界が開けるのだ。

公式暗記の手間が省ける

統一的観点を養えるということは、個々の事象に応じて公式を覚える必要がないことを意味する。

実際、微積分をマスターすれば暗記不要になる公式はいくらでもある。

例として、単振動を見てみよう。

単振動とは、円運動を直線上に射影したものであり、次の式で表せるのであった。

そして物理の教科書では、面倒な導出ののちに次のような速度・加速度の公式が載っている。

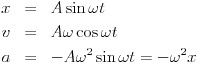
この公式を頭に入れるのに苦労している受験生は多い。

確かに少々複雑で、一目では覚えられない形をしている。

だが、驚くべきことにこの公式を覚える必要などないのだ。

ここまで読んだあなたならxの表式から残りの2つを導くことができる。

どうすればよいか、予想してみてほしい。

そう、時間微分だ。

を時間微分すれば速度は次のように計算できる。

加速度も同様に、速度を時間微分してやればよい。

こうして、x（位置）の式から速度と加速度を計算することができた。

つまり上の単振動の公式を覚える必要などないのだ。

xの式がsinではなくcosの場合にも、同様に微分してやれば良い。

柔軟に対応できるぶん、公式を覚えるよりもむしろ正確で簡単なのだ。

高校物理における微積分

というわけで、高校物理であっても微積分は大いに活躍する。

さらにいえば、公式暗記に頼って勉強するよりも微積分で物理的なものの見方を鍛えておいた方が、大学以降の学びの場で圧倒的に得をする。

高校物理で微積分を使うメリットをまとめると、

ということになる。

一旦微積分の使い方を身につけてしまえば、あとの学習がずっと簡単で楽しいものとなる。

また、大学以降の科学では微積分のスキルが大いに活躍するのは確実だ。

高校物理で微積分を使うデメリット

習得してしまえばいいことばかりに見える微積分。

だったらみんな微積分を使えばいいじゃないか、と思うに違いない。

だが、話はそこまで簡単ではないのだ。

次は、高校物理で微積分を使うデメリットについて考えてみる。

習得にかなりの数学力を要する

習得してしまえばありがたみがわかる微積分だが、そこに至るまでには大変な努力を要する。

微積分といっても数学IIのように単純な多項式を微積分するわけではなく、意味を持った物理量が対象になっているのだ。

したがって、いま自分がどういう計算をしているのかちゃんと理解しないことには意味がない。

先ほどの計算

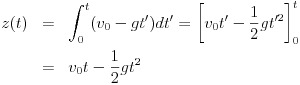
にしても、「速度を積分して位置を求めている」ということが分かっていないと、他の問題に応用することができない。

単に数学の道具を使って満足するだけでは無意味なのだ。

微積分を使えば、物理をシステマティックに、かつ統一的に理解できる。

だがその分、いま実行している計算の意味を抽象的に整理しないと訳が分からなくなるのだ。

そこそこ高級な数学を使う以上、その意味をしっかり理解する責任があることを忘れないようにしよう。

また、時には積分計算自体も少々難しいものとなる。

たとえば、先ほど紹介した単振動の公式

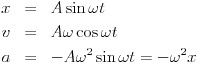
は確かに時間微分により計算できるが、その際実は合成関数の微分という数学IIIの範囲の計算を行なっていた。

時刻tは三角関数の中に入っているし、しかもωという係数が付いている。

したがってこの微分を実際にやるのは、高3レベルの数学力が要求されるのである。

一口に微積分するといっても、それを実行するのが大変なケースがあるということだ。

計算さえできれば話は簡単になるが、そこに至るまでに結構な数学力が前提となっている。

したがって、文系の受験生は手を出さない方が良い可能性が高い。

たとえ理系であっても、数学に自信がない人は微積分で物理を攻略するのを控えよう。

無理やり微積分を導入しても、却って混乱することになるからだ。

物理を統一的に、賢く学びたいと考えていて、かつ高3レベルの数学に自信がある人にはオススメである。

だがそれ以外の人にとっては　危険な勉強法でるのは確かだ。

すぐに結果が出ない

もう一つのデメリットは、勉強の成果がすぐに点数に反映されるわけではないということだ。

もちろん、統一的理解を志すこと自体は悪くないのだが、大学受験でそれを探求するのはあまりにコスパが悪いのである。

何ヶ月も真剣に物理・数学の勉強をしてはじめて、微積分を用いた物理の解釈が見えてくるのが普通だ。

古文単語の暗記などとは異なり、勉強し始めてすぐに結果が出ることはあり得ない。

長期にわたる努力が前提となっていることを肝に銘じてほしい。

また、理系の受験生であれば大学以降も科学の世界で微積分を使うことがあるだろうが、文系の受験生などは大学受験が終わったら理科と無縁になる人が多い。

そういう人が微積分を必死に勉強するというのは、苦労ばかり伴う作業になってしまう。

しかも、文系の人にとって微積分自体が楽な計算ではない。

繰り返しになるが、文系の受験生にはあまりお勧めできる攻略法ではない。

どうしてもコスパが極端に低くなってしまい、大学受験の勉強として不適切なスタイルになるためである。

高校物理で微積分を使うデメリット

デメリットについても、軽くまとめておこう。

高校物理を微積分で突破することのデメリットは、簡単にいうと次の通りだ。

ここからわかるように、微積分を使うというのは相当の「覚悟」が要求されているのである。

簡単な判断基準としては、次のように考えると良い。

もちろん、この基準は絶対ではない。

数学が苦手であっても、物理の良い理解のために微積分を使った物理に挑戦するのは良い姿勢である。

受験までの残り時間や数学力と相談して、どちらにするか慎重に判断してほしい。

まとめ

物理を微積分で理解する意味、高校物理で微積分を使うメリット・デメリットを説明した。

統一的で賢い理解は、微積分を使ってこそ得られるものである。

だが一方で、習得までのは多くの時間・労力を要する。

やるなら相当な覚悟で臨むようにしよう。

理系で数学に自信がある受験生は、是非挑戦してみよう。

一度習得してしまえば、以降の勉強はずっと楽になる。

そうすればどんな入試問題にも対処できる圧倒的な物理力を身につけることができるのだ。

自分の学力や進路と相談して、どちらを選ぶかよく考えてほしい。