物理が苦手な受験生に贈る、正しく着実な公式の勉強法

物理が苦手という場合は通常とは意味が違う。

たとえば英単語が苦手ならば、とにかく英単語を頑張って暗記すれば良い。

しかし、物理は時間をかければ良いという訳ではないのだ。 物理の苦手を克服するには、量をこなすよりも「物理的な考え方を理解する」ことが大切である。

では、「物理的な考え方」というのは何だろうか？ それを学ぶにはどうすれば良いだろうか？

今回は、物理の苦手意識を払拭して点を取れるようにするための勉強法を説明する。

いくら勉強しても視界が開けない受験生にとって、以下の説明は価値あるものに違いない。

これを読んで、物理がどういう科目なのか理解しよう。

物理は何のためにあるか

目的が明確でないまま努力をしても意味がない。 具体的な勉強法の話をする前に、そもそも物理は何のためにある科目なのかを理解しよう。

球の運動を例に

簡単な例として次の問題を考えよう。

＜例題＞ 鉛直上向きにy軸がくるようにxy平面を取る。 時刻0で原点から質量mの球を、初速v0、角度θで投射したとき、時刻tにおける物体の位置を求めよ。 ただし、重力加速度の大きさをとする。

物理を少し勉強すれば、これくらいの問題は容易に解けるようになる。 解答例は以下の通り。

＜解答例＞ 初速度のx成分、y成分はそれぞれである。 x方向へは等速度運動をするので  一方y方向へは等加速度運動をするので  となる。　■

答えはともかくとして、この問題で何をやったのか考えてみよう。

与えられていた情報は、時刻0で物体をどの位置からどのように投射したか、である。

そして最終的に求めたのは時刻tにおける物体の位置である。 時刻0というのは言ってみれば「最初」だ。

時刻0から見ると時刻tは「未来」である。 つまり、この問題は初期設定を元に物体の未来の運動を計算したのである。

このように、物理の大きな目的に一つは「未来を予測すること」である。 運動方程式を解くことで、物体の任意の時刻における位置を求めることができるのだ。

法則を知り、それを元に未来を予測する。 これはなにも大学受験に限った話ではなく、実際の研究も同様なのだ。

少ない法則で、多くのことを説明する

様々な現象から法則を見つけ出すのが物理の仕事だが、闇雲に法則を立てればよいという訳ではない。

物理学における法則は、以下の2点によって価値が決まる。

法則を立てたとしても、数が多すぎては使い勝手が悪い。 使いやすさ・明快さ・理論としての美しさという観点では、法則の数は少ないほうが望ましいのである。

また、法則の適用範囲が狭いと価値が低いものになってしまう。

たとえば物体の数が2個の場合にしか成り立たない法則よりは、物体が何個あっても成立するものの方が望ましい。

条件が厳しい法則は、そのぶん説明できる現象が少なくなってしまうので役に立ちにくいのである。

物理の法則として価値があるのは、上の二点を満たしているものである。 実際、東京大学の清水明という研究者は次のように述べている。

物理学は、自然現象について、できるだけ簡潔かつ普遍的な見方を見いだそう、という学問である。
ここで、「普遍的」というのは、ひとつの見方が、非常に広い範囲の自然現象にあてはまる、ということである。
たとえば、「星々の運動と、地球の上でリンゴが木から落ちることが、実はまったく同じ法則で記述できるのではないか」という見方をしてみる。
そして、そのことを、数学を用いて曖昧さなく記述してみる。
すると、驚くべき事に、星の運動もリンゴの運動も全く同じ方程式で記述でき、しかもその方程式が、大変に簡潔な形をしている。
これが、簡潔かつ普遍的な見方である。
しかも、そのようにすると、星でもリンゴでも、その運動についての観察や実験の結果が説明できるだけでなく、まだ観察や実験をしていない未来のこと（例えば、今から１００年後の月や星の位置）まで予言できてしまう。

清水研のHPより

文中の「全く同じ方程式」というのが大切。

たとえば万有引力という概念は、りんごが落ちるのも天体の運動も、同じ方程式で説明できたことに価値があるのだ。

このように「簡潔かつ普遍的な見方」を探求するのが物理学なのだ。

大学受験の物理はどういう科目か

物理は普遍的な法則を探す学問である。

したがって、大学受験の物理で登場する法則も、実は案外単純であるし数も少ない。

たとえば運動方程式はという単純な形をしているが、これだけでかなり多くの現象を説明することができる。

力学の分野でまともに覚えなければならないのはこの運動方程式くらいである。

力学に限らず、高校物理で登場する物理公式は少数なのである。

それなのに、物理が苦手な受験生は多い。

それは、公式の意味や使い方を理解していない人が多いためなのだ。

という式自体は誰でも覚えることができる。

小難しい英単語よりかはよほど単純な形をしている。

だが、この式が何と何の関係を示していて、実際にこれをどう用いるのかを知らないことには物理を理解したとは言えない。

地歴公民であれば、人物名や単語を知っているだけである程度価値がある。

たとえば大隈重信という人物名や彼の業績を知っているだけで、試験では点を獲得することが可能だ。

しかし物理では「知っている」だけでは何ら価値がない。

それを実際に適用して問題を解いて初めて、物理を勉強した価値があるのだ。

物理が苦手な受験生はこれを肝に銘じておこう。

ここまでのまとめ：物理が目指すもの

物理はどういう科目なのか、少しずつ見えてきた。

ここまでの内容を一旦まとめておこう。

とりあえずこの2点だけは頭に入れておこう。 物理の勉強をするときに、公式を覚えて満足してしまう受験生がいる。 それがマズいというのは、ここまで読んできたあなたなら理解しているに違いない。

公式を「理解」する

物理にはいくつかの基本公式が登場する。 それらを知っていれば原理的にはどんな問題も解けるのだが、実際は難しいことである。 大学入試問題を解くのに必要な力は何か、考えていこう。

何を主張している公式なのか考える

すでに登場したという公式を見てみよう。

この公式は何を主張しているのだろうか。

以下の説明を読む前に、あなた自身の言葉で説明してほしい。

まず、この公式に登場している文字が何を指しているかというと、

である。 公式の主張を理解する第一歩は、式に登場している物理量は何かを把握することである。

次に、それらの物理量がどういう関係になっているかを認識する。 ということは「力=質量×加速度」という関係であることを意味している。

つまりこの公式は、「物体にはたらく力は、その物体の質量に加速度をかけたものである」という意味の公式であることがわかる。

公式の「使い方」を考える

公式の意味を理解するというのは重要なステップだ。

しかしそれのみでは不十分で、その公式の「使い方」を理解する必要がある。

再びを例に考えよう。 これは「力=質量×加速度」という関係式であった。

この公式は、問題を解く時にどのように使えるだろうか。 まず考えられるのは、質量と加速度を知っているときに力を求めるという使い方だ。

1 kgの物体が1メートル毎秒毎秒で加速しているとしたら、その物体にはたらく力は1 × 1 = 1 Nというふうに求められる。

しかし、それだけではない。 見方を変えれば、質量と力がわかっているときに加速度を求めることもできる。

10 kgの物体に100 Nの力を加えたら、その物体は100 ÷ 10 = 10 メートル毎秒毎秒で加速する、といった感じだ。

あるいは加速度と力がわかっているときに質量を求めることも可能である。 運動方程式は、力を求めるためだけにある公式ではない。

あくまで1つの関係式なので、見方によっては違う意味を持つのだ。

このように、物理の公式は条件設定・見方によって複数の使い方ができることも忘れないでおこう。

そうでないと、狭い思考に囚われてしまってなかなか問題を解けなくなる。

物理が苦手な受験生は、「運動方程式＝力を求める式」や「状態方程式＝体積を求める式」というふうに固定化された見方をしがちだ、

成立条件を見極める

公式の意味や使い方を理解するだけで解ける問題はたくさんある。

だが、もう一つ注意しなければならない点がある。

それは公式の「成立条件」だ。 例として運動量保存則を挙げる。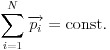 

運動量保存則は、系の運動量が保存するという法則である。 これを利用して、重心の速度が一定であることなどを示すことができ、物理の重要法則の一つだ。

だが、どんな場合にもこれを使えるというわけではない。 運動量保存則には成立条件がある。

それは、「外力がない」ということだ。 外力というのは系の外から加わる力のことである。

逆に、系の内部で物体同士で作用する力は内力という。

内力が作用している分には、運動量保存則は問題なく成立するのだが、外力が加わるとこれは成立しないのだ。

たとえば球の衝突を考えるときに、外から手で力を加えているのに運動量保存則を使うのは大きな誤りである。

物理の問題が解けない人の中には、このように公式だけが独り歩きしてしまい成立条件を見失っている人が大変多い。

その公式はどういうときに使って良いのか。 それを知ることも、問題を解く上で忘れてはならない。

公式を身につける3要件

公式を身につけるというのは、公式を暗記するということではない。 以下の3要件を満たしていることが必要なのだ。

これらに注意すれば、公式を適切な場面で使って問題を解くことができる。 物理公式を学ぶ際は、どれか1つでも欠かさないよう心がけよう。

問題を解くには

公式を学ぶ際の注意点を述べた。 次はいよいよ、具体的な勉強法について説明する。 物理が苦手な人ほど、最初の段階では丁寧に学習することを心がけよう。

まずは教科書

先述の通り物理では覚えるべき公式がかなり少ないので、初学者はいきなり問題集に取り組みたくなってしまう。

しかも、公式を暗記してしまえば最初のうちは問題を解ける。 それゆえ理解したつもりになり、どんどん先へと進んでしまうのである。

だが、そういう向こう見ずな勉強だといつか壁に突き当たることになる。

公式の意味を理解せずに文字列だけ頭に入っている状態だと、難易度が高い問題に対処できないのだ。

ただ単純に球を投げたり物体を滑らせたりするような問題は解けるだろうが、複数の物体が衝突したりバネが登場したりすると解けなくなっていく。

問題が複雑になると、どこでどの公式を使えば良いのかわからなくなるからである。

したがって、最初の問題が簡単だからといっていきなり問題演習に入るのは見た目以上に危険な方法である。

どんな科目でも共通して言えることだが、まずは教科書を読むことから始めよう。

教科書には、運動の三法則や運動方程式など初歩的な内容についても詳しく載っている。

上に述べた公式の意味や成立条件についても、欠かすことなく述べられているのだ。

教科書を落ち着いて読むことで、物理公式の正しい理解ができる。

簡単な例題も載っているので、公式の使い方が少しずつ分かるように設計されている。

受験勉強をする人は教科書をバカにしがちだが、教科書ほど丁寧で整った教材はない。

特に理科では基礎固めに教科書を読む習慣をつけよう。

簡単な問題を解こう

教科書を読んだら、次は簡単な問題から解いていこう。

たとえば運動量保存則を学んだとしたら、2つの物体の衝突の問題を解くのだ。

このとき重要なのは、なるべく単純で平易な問題を解くことである。

たとえば摩擦があるように複雑な問題はいま解くべきではない。

それはなぜかというと、最初はその公式1つを理解するのが先決だからである。

運動量保存と摩擦の両方が絡むような問題を解いていると、どこでどの法則を使えば良いのかわからなくなってしまう。

複雑であればあるほど、1つの公式に焦点を当てる時間は当然減るのだ。

したがって、最初のうちはいま注目している公式だけを使えば解ける問題をチョイスしよう。

学校で配られている問題集があるならそれを使えば良い。 自分で簡単な問題集を買って、その最初の問題を解いても良い。

とにかく、式1,2本であっさり答えが出るような問題を解いてみるのだ。

それは実際の大学入試問題とはかけ離れているだろうが、公式の意味や使い方を理解するうえでは最適な勉強法である。

複合問題を解く

その公式の意味や使い方がわかってきたら、次は複合的な問題を解いてみる。 複合的な問題とは、たとえば次のようなものだ。

＜例題＞ 質量mの球Aと質量Mの球がある。 Aは右向きに速さv1、Bは左向きに速さv2で同じ直線上を運動していた。 両者が衝突した後のAの速さを求めよ。 ただし、反発係数をeとする。

この問題を解くためには、運動量保存則と反発係数の双方の理解が必要だ。

式を1度使って答えが出るような問題でもない。

運動量保存則と反発係数の2つを使わなければ解けないため、この問題は複合的であるといえる。

当然、前の問題よりも複雑で難易度は上がる。

しかしこうして少しずつステップアップすることで、公式の使い方をマスターしていけるのだ。

さらなる難問へ

複合的な問題が解けるようになったら、問題集の中でも難しいものに手を出してみよう。

実際の大学入試問題は複雑な設定であり、どこでどの公式を使えば良いのか一目ではわからないことが多い。

そういう問題にも対応できる力を養うために、応用問題の演習は欠かせない。

題材としては、中堅校の過去問や全国模試が良い。

難しさを追求した問題集もいくつか存在するが、その多くはいたずらに難しい問題や奇問を含んでいる。

大学入試で必要なのは難問・奇問を解く力ではなくシンプルな条件設定の下で答えを出す力だ。

多くの人が挑戦する全国模試や大学の過去問は変な問題が少なく、良い演習題材となる。

このレベルに手を出せるようになれば、もはや物理は苦手ではなくなっているといえよう。

問題演習の際の注意点

物理の学習をする際に気をつけるべき具体的なポイントを述べておく。

まず、答えだけでなく途中式を必ず書くようにしよう。

物理ではたいていの問題は計算なしには答えを出せない。 答えだけノートに記すのは意味がないのである。

自分がどのように問題を解いたのか、記録が残らない。 しかも出した答えが間違っていたときに、どこで誤ったのかを判別できない。

計算問題では特に、途中過程を必ず書き残すようにしよう。 そして、計算の際にはどの法則を使ったのか明記すると良い。

たとえばエネルギー保存則を使ったときは、計算の前に＜エネルギー保存則＞のように付記しておくのだ。

こうすることで、どういう目的でどの公式を用いたのかが明確になり、公式の意義を理解しやすくなる。

また答案としてもその方が得点しやすい。 というのも、採点官はあなたがどの公式を使おうとしているのか知らないからだ。

急に数式から始まってしまったら、「なんだ、これは？」と驚いてしまう。

だが＜エネルギー保存則＞と書いてあれば式の意味をすぐに納得できる。

自分にとっても採点官にとっても価値があるので、これをやらない手はない。

問題演習の際はこれら2点を心がけよう。

まとめ

物理が苦手な人に向けて、物理は何のためにあるのか、公式を「身につける」とはどういうことなのか、といったことを説明してきた。

物理が苦手な人の多くは、公式を単なる文字列に近い形で覚えてしまっている。 だがそれは実践とはかけ離れており、問題を解く力には結びつかない。

公式の意味や使い方、成立条件を理解して初めてその公式を理解したことになるのだ。

正しい学習法で公式を着実に「身につけ」、苦手を克服していこう。